Falls es zu Fehlern beim laden von Bilder oder sonstigen Inhalten kommt (Ladezeichen), kann es helfen mit dem Mauszeiger auf den ladenden Inhalt zu drücken (Linke Maustaste).

Inhaltsverzeichnis:

• Mitternachtsformel
• Quadratische Funktionen
• Bestimmen Extremaler Werte
• Binomische Formeln
• Normaldarstellung (Wissenschaftliche Darstellung) [Potenzen]
• Exponentialgleichung (Logarithmus)
• Exponentielles Wachstum
• Verdopplungs- / Halbwertszeit
• Berechnungen am Rechtwinkligen Dreieck
• Sinus, Kosinus, Tangens
• Körper
  • Quader
  • Zylinder
  • Quadratische Pyramide
  • Kegel
  • Kugel
• Stochastische Unabhängigkeit
• Sonstiges

Mitternachtsformel

Habt ihr eine Gleichung in dieser Form, dann setzt ihr a, b und c in folgende Formel ein.

Dabei ist:

• a immer die Zahl vor dem x hoch 2.
• b immer die Zahl vor dem x (ohne hoch 2)
• c immer die Zahl ganz ohne x

Das ± bedeutet, dass ihr die Formel zweimal rechnen müsst, nämlich einmal mit – und einmal mit +. Es kann nämlich bei quadratischen Gleichungen zwei Lösungen geben. Beispiele findet ihr weiter unten.

Wichtiger Hinweis: Sollte unter der Wurzel etwas negatives rauskommen, dann hat diese Gleichung keine Lösung. Es gibt also keinen Wert für x, wofür die Gleichung dann 0 ergibt.

Beispiele

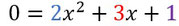
Ihr habt diese Gleichung gegeben.

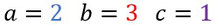
Bestimmt jetzt a, b und c. 

Setzt die Werte für a, b und c in die Mitternachtsformel ein und vereinfacht so weit wie möglich. 

Jetzt berechnet ihr es einmal für + und einmal für –. Nun habt ihr beide mögliche Lösungen. Übrigens ist es egal, ob bei x1 oder x2 minus/plus gerechnet wird. 

Bilder von studimup

Selbst üben

Übungen zu Mitternachtsformel

Quadratische Funktion

Aufschrieb HerunterladenAnwendungHerunterladenAnwendungHerunterladen

Normal Parabel

Der Graph einer quadratischen Funktion ist eine Parabel

Der Graph mit der Vorschrift y=x² heißt Normalparabel mit dem Scheitel S(0|0). Die Normalparabel ist nach oben geöffnet.

Allgemeine Form

f(x)=ax²+bx+c | Der Streckfaktor a kann aus beiden Gleichungen abgelesen werden

Ist eine Parabel gestreckt gilt im Vergleich zur normal Parabel:

a > 1	nach oben geöffnet	enger als die Normalparabel
0 < a < 1	nach oben geöffnet	weiter als die Normalparabel
-1 < a < 0	nach unten geöffnet	weiter als die Normalparabel
a < -1	nach unten geöffnet	enger als die Normalparabel

Scheitelform

f(x)=a(x−d)²+e | Hier kann der Scheitel abgelesen werden S(d | e)

Auch hier gilt die oben stehende Tabelle

Wird eine Parabel mit dem Scheitel S(0 | 0) im Koordinatensystem um d in x-Richtung und um e in y-Richtung verschoben, hat die verschobene Parabel die Gleichung f(x)=a(x−d)²+e

Von der allgemeinen Form zur Scheitelform

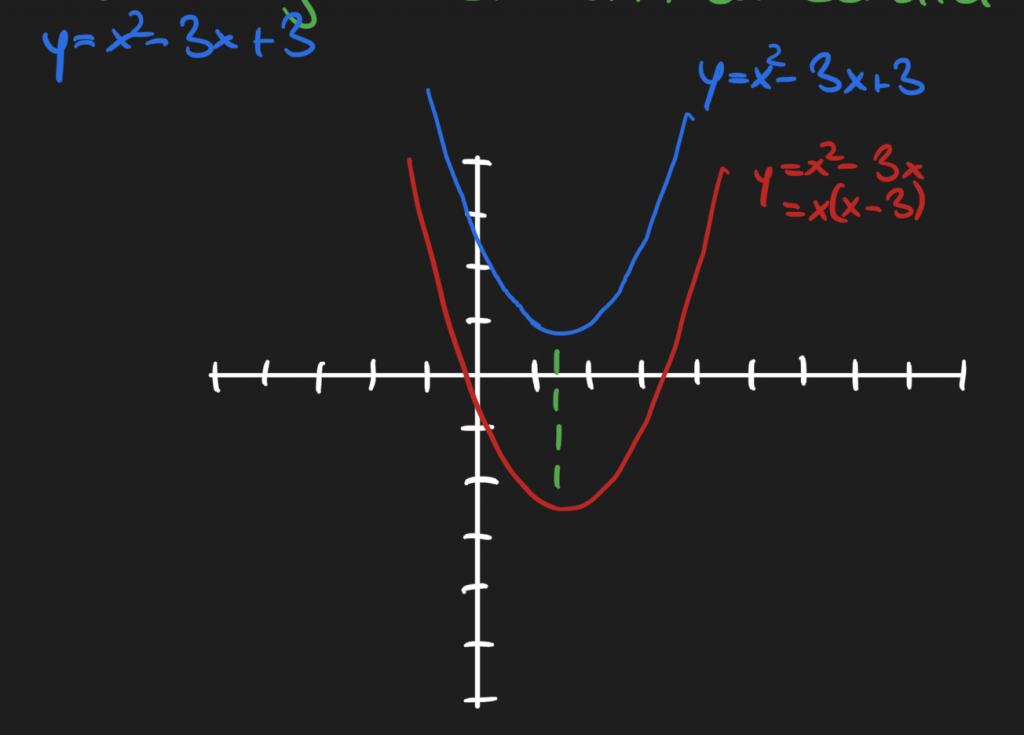
Vorgehen

1. Verschiebe die Parabel so, dass sie durch den Ursprung verläuft. Also um -3 in y-Richtung
   y=x²-3x
2. Bestimme die Nullstellen
   y=0
   => x²-3x = 0
   x * (x-) = 0
   
   Satz vom Nullprodukt: x1 = 0, x2 = 3
3. Bestimme daraus den x-Wert des Scheitels. xS = 1,5 denn der Scheitel liegt genau zwischen den Nullstellen
4. y-Wert bestimmen in dem man xS einsetzt
   y=x²-3x+3
   x2=1-5
   => y=1,5²=3*1,5+3
   y=0,75
   => S(1,5 | 0,75)
5. Scheitelform: y=a*(x-d)²+e
   y=a*(x-1,5)²+0,75

Selbst üben

Übungen zu Quadratischen Funktionen

Bestimmen extremaler Werte

HeftaufschriebHerunterladen

Aufgabe
Geg: 20m Drahtzaun
Ges: Bei welcher Breite wird das Gehege maximal groß

Allgemeines Vorgehen

1. Wie lautet eine Formel für die Größe die extremal werden soll?
2. Drücke die gesuchte Größe in einer einzigen Variablen aus
3. Bestimme das Maximum bzw. Minimum der Zielfunktion
4. Formuliere eine Antwort auf die gestellte Frage

Auflösung der Aufgabe

1. A=a⋅b
2. a=20-2⋅b
    A=(20-2⋅b)⋅b
    A=20b-2b²
3. Nullstellen bestimmen
    A=0
    20b-2b²=0
    b⋅(20⋅2b)=0
    b1=0
    b2=10
    bS=5 (Scheitelpunkt)

Ergebnis: Die Breite des Geheges sollte 5m betragen, damit es den größt möglichen maximal Wert hat.

Binomische Formeln

1. (a+b)² = a²+2ab+b²
2. (a-b)² = a²-2ab+b²
3. (a+b)*(a+b)=a²-b²

Normaldarstellung (Wissenschaftliche Darstellung) [Potenzen]

Potenzen-mit-ganzen-HochzahlenHerunterladenPotenzen-mit-gleichen-GrundzahlenHerunterladenPotenzieren-von-PotenzenHerunterladen

Man benutzt diese Darstellung mit Zehnerpotenzen um sehr große / sehr kleine Zahlen darzustellen.

1. Gewicht der Erde
   5,972⋅10²⁴ = 59720000000000000
2. 1,43⋅10^-6mm = 1,43 ⋅ (1:10⁶mm) = 0,00000143

Exponentialgleichungen (Logarithmus)

Arbeitsblatt aus dem UnterrichtHerunterladen

Der Logarithmus zur Basis 2 von 8, man schreibt dafür log₂(8), ist diejenige Zahl, mit der man 2 potenzieren muss, damit man 8 erhält: log₂(8) = 3, da 2³ = 8

Exponentielles Wachstum

Exponentielles-WachstumHerunterladen

Wichtige Begriffe:

P: Prozentuale Änderung pro Zeiteinheit
a: 1+p

• „Zerfall“: p < 0
  
  Abnahme um 2,5% –> -0,025
  a = 1-0,025 = 0,975
• „Wachstum“: p > 0
  Wachstum um 35% –> 0,35
  a = 1+0,45 = 1,35

Verdopplungszeit / Halbwertszeit

Verdopplungszeit / HalbwertszeitHerunterladen

Verdopplungszeit

^Tv: Feste Zeitspanne, bei der sich der Bestand (Bei a > 0) verdoppelt
Es gilt:

c⋅a^t+T_v = 2⋅c⋅a^t
c⋅a^t⋅a^T_v = 2⋅c⋅a^t
a^T_v = 2

T_v = Log_a(2)

Halbwertszeit

^T_h: Feste Zeitspanne, in der sich der Bestand (bei a < 0) halbiert
Es gilt:

c⋅a^t+T_h = 0,5⋅c⋅a^t
c⋅a^t⋅a^T_h = 0,5⋅c⋅a^t
a^T_h = 0,5

^T_h = log_a(0,5)

Berechnungen am rechtwinkligen Dreieck

HeftaufschriebHerunterladen

1. Der Satz des Pythagoras: a²+b²=c²
   Gegeben ist ein Dreieck mit den Seitenlängen a,b und c. Wenn das Dreieck rechtwinklig mit der Hypotenuse c ist, dann gilt a²+b²=c²
2. Umkehrung
   Gegeben is ein Dreieck mit den Seitenlängen a, b und c, wenn a²+b²=c² gilt, dann ist das Dreieck rechtwinklig mit der Hypothenuse c.

Für Beispiele siehe Datei „Heftaufschrieb„

Sinus, Kosinus und Tangens

Sinus, Kosinus, TangensHerunterladen

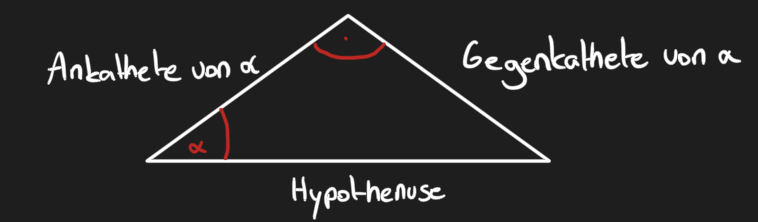
Definition: In einem rechtwinkligen Dreieck nennt man zu einem Winkel α des Dreiecks das Streckenverhältnis

Sinus
sin(α)=Gegenkathete von α : Hypotenuse

Kosinus
cos(α)=Ankathete von α : Hypotenuse

Tangens
tan(α)=Gegenkathete von α : Ankathete von α

Für Beispiele siehe Datei „Sinus, Kosinus, Tangens„

Wichtiger Hinweis: Um mit dem Taschenrechner den Sinus, Kosinus oder Tangens zu berechnen muss er auf dem modus deg (degree) sein.

Hier eine Anleitung falls der Taschenrechner nicht auf „DEG“ steht:

Du kannst es versuchen mit SHIFT und SETUP,
weil du möglicherweise MODE gar nicht findest.

SHIFT und SETUP sind höchstwahrscheinlich in der obersten Reihe.

Dann WINKELEINHEIT , vermutlich 2

Und dann 1 oder 2 oder 3 nach Bedarf.

VORSICHT: Hinterher wieder zurückschalten!
Im Gegensatz zu anderen Taschenrechnern behält CASIO diese Einstellung,  selbst wenn das Gerät ausgeschaltet wird.

Ggf. testen: sin 30° = 0,5 zeigt er nur bei DEG(REE).

Quelle

Körper

Alle Bilder von Abiweb dort können auch noch weitere Körper gefunden werden.

Kreis

Satz: Für den Umfang eines Kreises mit dem Radius r bzw. dem Durchmesser d gilt
U = 2⋅π⋅r oder U = π ⋅ d
Satz: Für den Flächeninhalt eines Kreises mit dem Radius r gilt
A=π⋅r²

Für die Kreiszahl π gilt näherungsweise π = 3,14

* ein Kreis ist kein Körper (Der Körper zum kreis wäre die Kugel)

Quader

O = 2⋅(a⋅b+a⋅c+b⋅c)
V = a⋅b⋅c

Zylinder

A_Grundfläche=A_Deckfläche=π⋅r²

U_Grundfläche=UDeckfläche=2⋅π⋅r

A_{Mantelfläche}=U⋅h=2⋅π⋅r⋅h

O_Zylinder=(2⋅π⋅r2)+(2⋅π⋅r⋅h)

V_Zylinder=Grundfläche⋅Höhe=π⋅r²⋅h

Quadratische Pyramide

A_Grundfläche=a²

A_Mantel=4⋅(1/2⋅a⋅h_Dreieck)

O_Pyramide= Grundfläche + Mantelfläche =a²+4⋅(1/2⋅a⋅h_Dreieck)

V_Pyramide=1/3⋅a²⋅h_Pyramide

Kegel

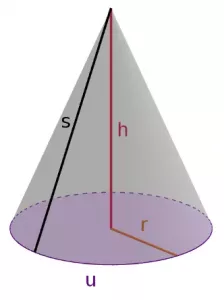
U_Grundfläche=2⋅π⋅r

A_Grundfläche=π⋅r²

A_{Mantelfläche}=π⋅r⋅s

O_Kegel=G+M=(π⋅r²)+(π⋅r⋅s)

V_Kegel=1/3⋅(π⋅r²)⋅h

Kugel

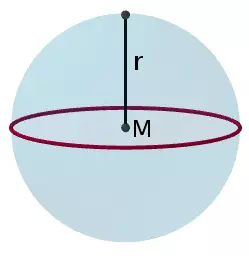
UKugel=2⋅π⋅r=π⋅d

OKugel=4⋅π⋅r²

VKugel=4/3⋅π⋅r³

Stochastische Unabhängigkeit

In manchen Situationen gilt, dass Pa(B) = P(B) für zwei Ereignisse A und B ist. In diesem Fall nennt man A und B unabhängig, andernfalls nennt man A und B stochastisch abhängig. Die Ereignisse A und B sind genau dann stochastisch unabhängig wenn die Formel
P(AnB) = P(A)*P(B) gilt
Sind in einer Vierfeldertafel die Wahrscheinlichkeiten notiert, kann man die stochastische Unabhängigkeit der Ereignisse A und B prüfen, indem man überprüft ob im Feld für die Wahrscheinlichkeit P(AnB) gerade das Produkt P(A)*P(B) stehtStochastische UnabhängigkeitHerunterladen

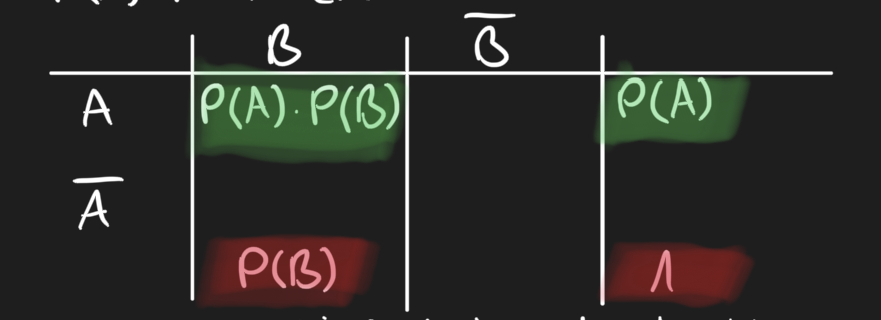
Sind in einer Vierfeldertafel die absoluten Häufigkeiten eingetragen, überprüft man den Quotienten der grün makierten Felder gleich dem der roten Felder ist

Sonstiges

Wer nochmal alle Grundlagen aus der 7. Klasse anschauen möchte, kann in diesem Dokument alles zu den folgenden Themen noch einmal nachlesen

Mathematik-Grundwissen-10.-KlasseHerunterladen